이차원 배열 탐색(CNN 아이디어)

< 문제 >

정해진 모양에 따른 탐색 문제

 

mxn 이차원 배열에서 다음과 같이 3x3모양의 H 혹은 L (이 문제에서는 H 라 가정)이 훑을 때

H자에 포함되는 숫자들의 합의 최댓값을 구하시오

(입력을 받는 것이 원칙이지만 편의상 아래의 행렬을 고정으로 받는다고 가정하자)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

< 이론 >

이차원 배열 slicing하기

- 이차원 배열이 나오는 순간 그냥 numpy를 이용하자

 

예시로 input이 다음과 같을 때

input = [[1,2,3,4,6],
        [3,4,2,3,5],
        [1,2,3,4,6],
        [1,2,3,4,6],
        [1,2,3,4,6]]

만약 이걸 3X3으로 자르고 싶다면

import numpy as np
np_input = np.array(input)
slicing_array = np_input[0:3,0:3]

 

이렇게 slicing할 수 있다

>>>
[[1 2 3]
[3 4 2]
[1 2 3]]

 

결론은

slicing_arr = two_dim_arr[ x_bound , y_ bound]
slicing_arr = two_dim_arr[x_bound][y_bound]

 

 

 

 

 

Matrix 내적 & 원소들의 곱 (+) dot , @, * 

- 내적은 결과값이 스칼라 값이 아닌 백터값이 나온다

곱은 원소 끼리의 곱(Dot product) 와 행렬의 곱(matrix multiplication) 이 있다다

(외적은 왜 안하냐 하는데 코테 볼 때 외적까지 떠올리는 천재는 아니기에... 버린다, 사실 matmul 도...)

 

코테에서 응용하기에는 Element-wise product 밖에 없는거 같으니 이걸 중점적으로 공부하자

 

같은 위치의 원소들 끼리의 곱 (Element-wise product) : np.multipy , *

https://numpy.org/doc/stable/reference/generated/numpy.multiply.html

numpy.multiply — NumPy v1.24 Manual

 

위에서 numpy를 이용하기로 했으므로 numpy 위주로 살펴보면

두가지 사용법이 있다

 

1. np.multiply(mat1, mat2)

 

input1 = [[1,2,3],
          [1,2,3],
          [1,2,6]]

kernel = [[1,0,1],
          [1,1,1],
          [1,0,1]]

element_wise_mul = np.multiply(input1,kernel)
print(element_wise_mul)

np.multiply의 장점은 numpy로 변환할 필요없이 list도 취급을 한다는 것이다

 

 

 

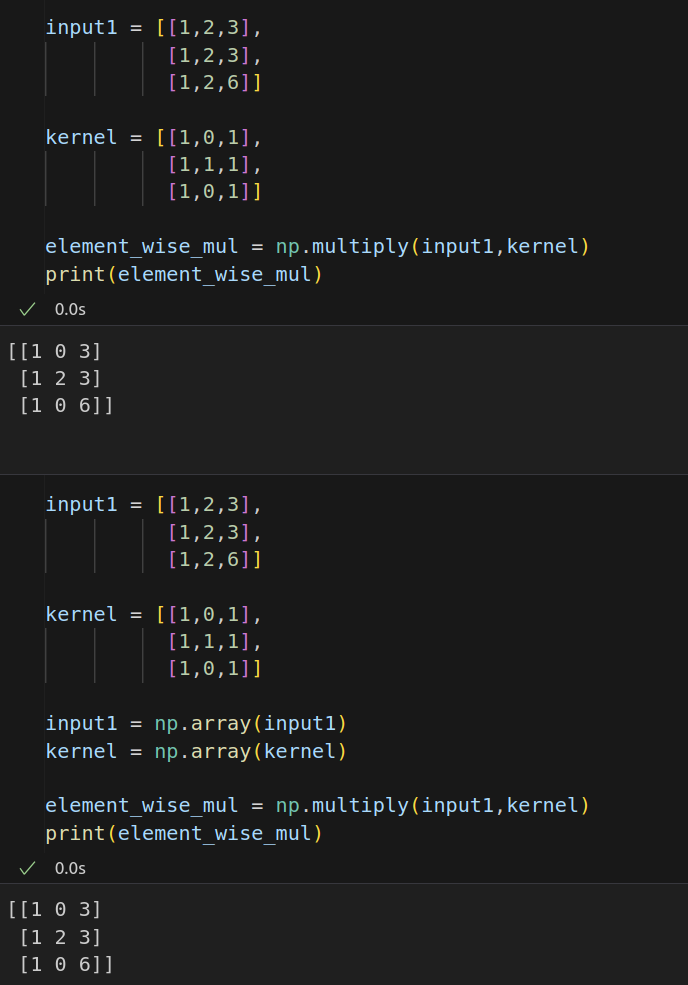
2. mat1 * mat2

input1 = [[1,2,3],
          [1,2,3],
          [1,2,6]]

kernel = [[1,0,1],
          [1,1,1],
          [1,0,1]]

input1 = np.array(input1)
kernel = np.array(kernel)

element_wise_mul = input1 * kernel
print(element_wise_mul)

* 연산자를 이용하는 것의 장점은 간단하다는 것이다

하지만 list를 취급하지 않으므로 numpy 변환과정이 필수이다

 

<주의 점>

파이썬에서는 나름 장점이라고 만들었는데

독이 되는 기능들이 바로 브로드 캐스팅이다

 

다행히도 * 연산 같은 경우는 벡터와 같이 차원이 1 이 섞여있는 경우만 broadcasting을 지원한다

ex)
(1,m) * (n,m) = (n,m)
(m,1) * (m,n) = (m,n)

어려워 보이지만 그냥 상수만 곱해지는 것이 가능하다라고 생각하면 된다

이런 식으로

 

 

 

Matric 내적 (inner product, dot product) : dot

실제 코테에서는 dot product를 쓸 일이 그리 많을 것 같지 않지만

위에 * 와 헷갈리기 때문에 한번 정리하고자 한다

A_matric = (m , n)
B_matric = (n , l)

A_matric.dot(B_matric)   -------> (o)
B_matric.dot(A_matric)   -------> (x)

와 같이 가운데의 차원이 같아야 연산이 가능하고

교환법칙이 성립하지 않는다

input1 = [[1,2,3],
          [1,3,3],
          [1,7,6]]


kernel = [[1],
          [1],
          [0]]
input1 = np.array(input1)
kernel = np.array(kernel)

element_wise_mul = input1.dot(kernel)
print(element_wise_mul)

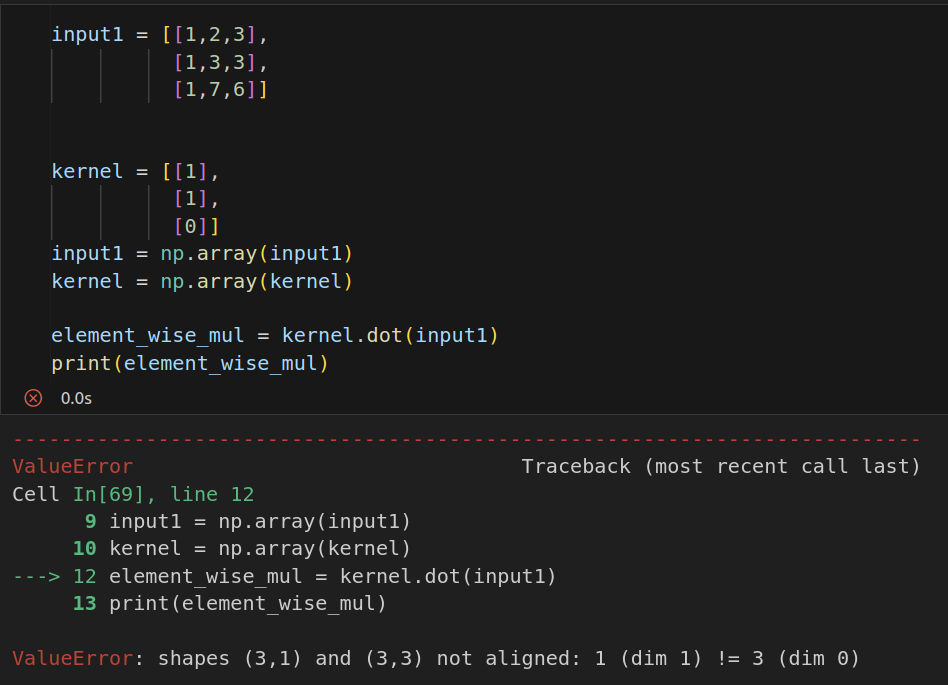
딱 이정도만 알면 될 것 같다

 

 

 

 

행렬의 곱 (Matrix Multiplication) : np.matmul , @

진짜 우리가 아는 행렬의 곱이다

 

근데 저 위의 그림을 보면 다음과 같은 의문점이 들 것이다

"내적이랑 같은거 아니야??"

이는 반은 맞고 반은 틀린 말이다

 

2차원 배열에서는 내적(dot)과 행렬의 곱(matmul, @)의 결과가 같다

 

3차원부터는 외적을 하게 되기때문에 달라진다

(AI를 다룰 때는 고려사항이 되지만 코테에서 굳이 행렬의 곱까지 다룰 필요가 있을까 라는 생각을 한다)

 

그래도 정리하는 김에 해보면

 

공식문서 에서는

numpy.matmul(x1, x2, /, out=None, *,
                         casting='same_kind', order='K', dtype=None, subok=True[, signature, extobj, axes, axis])

로 나와있긴 하지만 저걸 어캐 다 기억합니까

 

그냥 한번 사용해보는 걸로 만족합시다

input1 = [[1,2,3],
          [1,2,3],
          [1,2,6]]

kernel = [[1,0,1],
          [1,1,1],
          [1,0,1]]

input1 = np.array(input1)
kernel = np.array(kernel)

inner_prod = input1.dot(kernel)
matrix_mul = input1@kernel
print(matrix_mul , "\n")
matrix_mul = np.matmul(input1,kernel)
print(matrix_mul , "\n")
print(inner_prod)

셋다 동일한 결과를 얻을 수 있습니다

 

 

 

 

 

 

 

 

< 문제  풀이>

1. 직관적인 풀이

input = [[1,2,3,4,6],
        [3,4,2,3,5],
        [1,2,3,4,6],
        [1,2,3,4,6],
        [1,2,3,4,6]]


import numpy as np

kernel = [[1,0,1],
          [1,1,1],
          [1,0,1]]
output = [] #Dynamic programming

kernel_size = len(kernel)
output_row_size = len(input[0])-len(kernel[0])+1
output_col_size = len(input)-len(kernel)+1


for col in range (output_col_size):
    for row in range (output_row_size):
        tmp = (input[col][row] + input[col+1][row] + input[col+2][row]
               + input[col+1][row+1]
               + input[col][row+2] + input[col+1][row+2] + input[col+2][row+2])
        output.append(tmp)
        
print(max(output))
output

그냥 H 자를 다 덧셈으로 더한 값을 Dynamic programming으로 구현 한 것이다

 

이게 비효율적으로 보이지만 실제 코딩테스트에서는 Slicing이니 행렬이니 다 필요없이

빠르게 답을 구해내는 것이 중요하기에 마땅한 아이디어가 없었으면 이렇게 풀었어야 한다

 

 

2. 행렬의 연산을 이용한 풀이

input = [[1,2,3,4,6],
        [3,4,2,3,5],
        [1,2,3,4,6],
        [1,2,3,4,6],
        [1,2,3,4,6]]



import numpy as np

kernel = [[1,0,1],
          [1,1,1],
          [1,0,1]]
output = [] #Dynamic programming


np_input = np.array(input)
np_kernel = np.array(kernel)

kernel_size = len(kernel)
output_row_size = len(input[0])-len(kernel[0])+1
output_col_size = len(input)-len(kernel)+1


def array_sum(arr):
    ans =0
    for col in range(len(arr)):
        for row in range(len(arr[0])):
            ans += arr[col][row]
    return ans


for col in range (output_col_size):
    for row in range (output_row_size):
        slicing_array = np_input[col:col+kernel_size,row:row+kernel_size] #slicing
        output.append(array_sum(np_kernel*slicing_array)) #out_element

print(max(output))

가장 파이소닉하게 푼 풀이이다

하지만 실제 구현에 있어서는 1번 보다 조금 더 시간이 오래걸리지만 실수의 확률이 줄어들어서 괜찮은 풀이같다

(위에 이론을 모르거나 헷갈리는게 있으면 빠르게 접고 1번과 같이 풀어야한다)

 

 

 

3. Pytorch (CNN)을 이용한 풀이

computer vision을 공부했다면 문제를 보고

CNN을 떠올렸을 것이다

만약 torch가 import 가 된다면 다음과 같이 풀 수도 있지만

구현보다 차원을 맞추고 parameter 형식을 맞추는 것이 더 오래 걸려 비효율적이지만

간지는 난다

 

Convolution Neural Network (CNN)

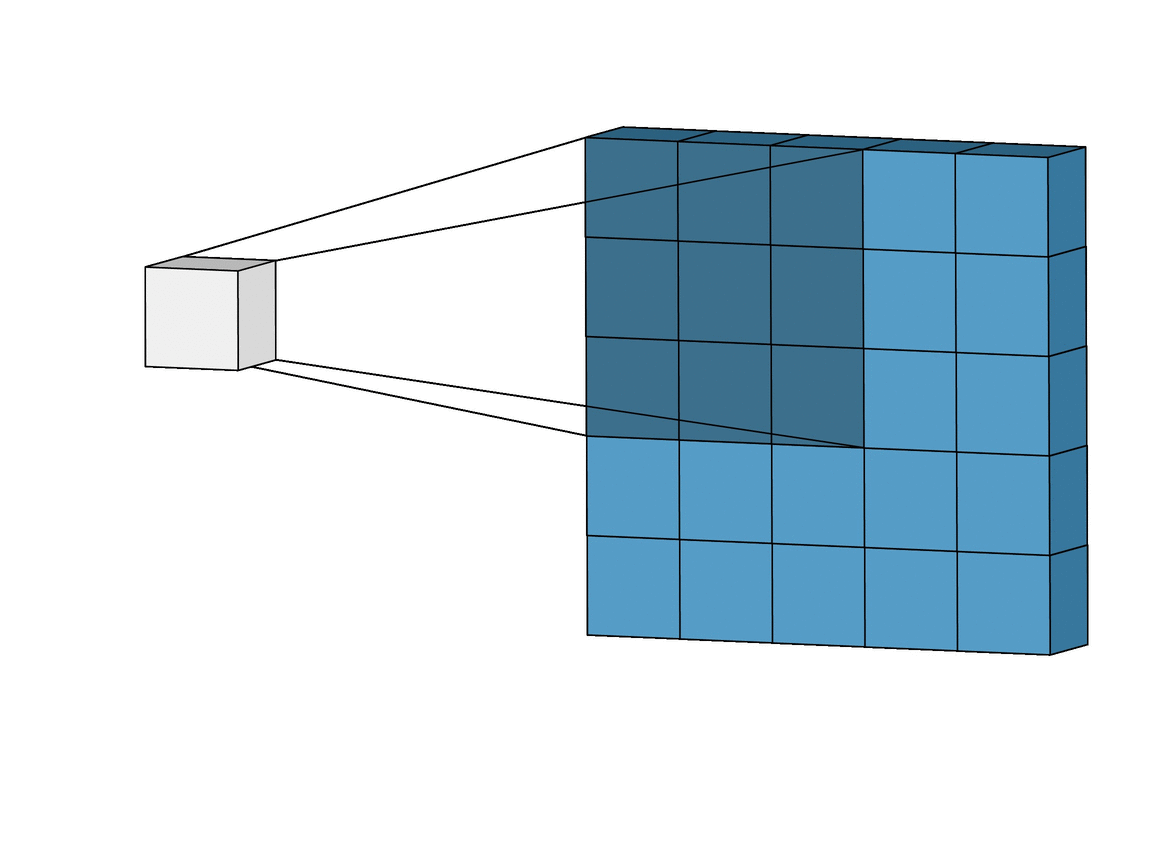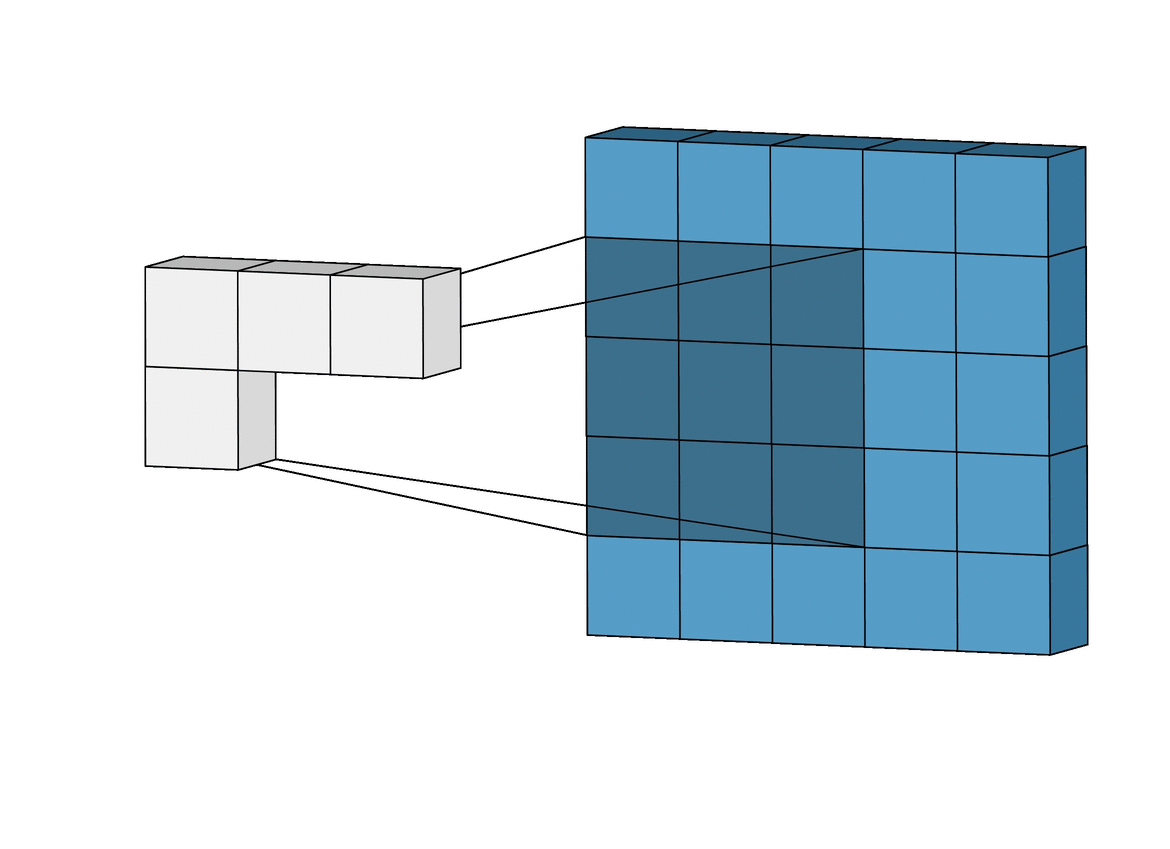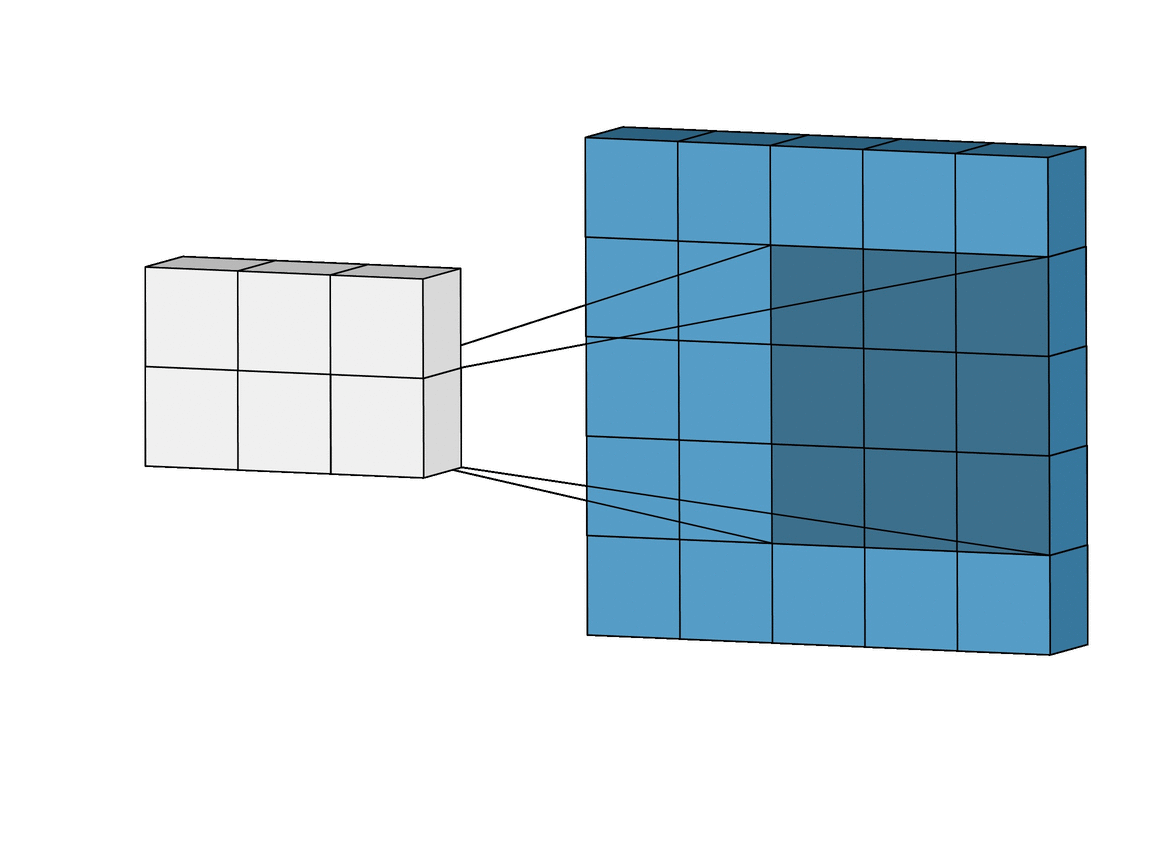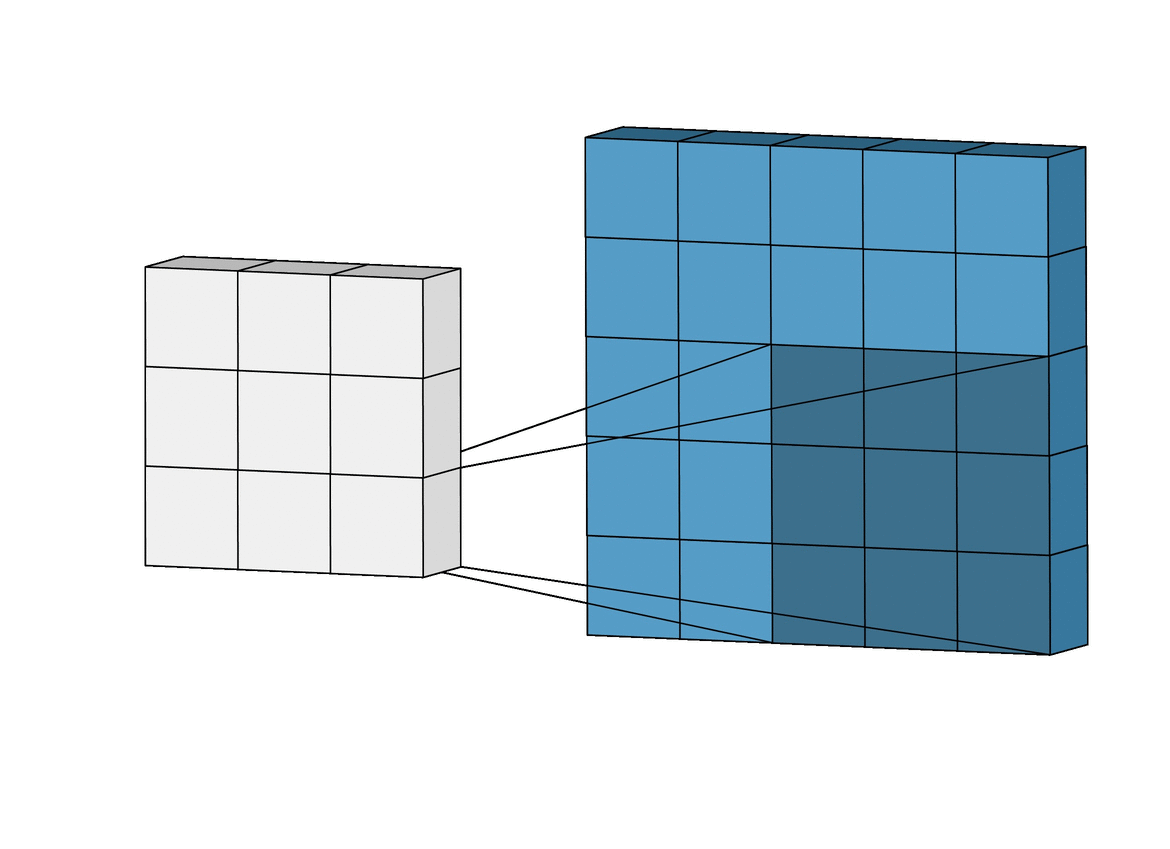
import torch
import torch.nn as nn
import numpy as np


input1 = [[1,2,3,4,6],
          [3,4,2,3,5],
          [1,2,3,4,6],
          [1,2,3,4,6],
          [1,2,3,4,6]]

kernel = [[1,0,1],
          [1,1,1],
          [1,0,1]]

input1 = np.array(input1)
kernel = np.array(kernel)




conv = nn.Conv2d(in_channels=1, out_channels=1, kernel_size=3,padding=0,stride=1)
input1=torch.from_numpy(input1[np.newaxis,np.newaxis,:,:]).float()
conv.weight = nn.Parameter(torch.from_numpy(kernel[np.newaxis,np.newaxis,:,:]).float()) #parameter를 써야 weight로 들어간다
#print(conv.weight, conv.weight.size())

feature_map = conv(input1)

print(int(feature_map.max()))

 

 

 

 

 

 

 

https://numpy.org/doc/stable/reference/generated/numpy.matmul.html

numpy.matmul — NumPy v1.24 Manual

https://seong6496.tistory.com/110

[Numpy]행렬곱(@)과 내적(dot) 그리고 별연산(*)

https://numpy.org/doc/stable/reference/generated/numpy.multiply.html

numpy.multiply — NumPy v1.24 Manual