[DL Basic] NN & MLP
<Neural Networks>
인공 신경망 즉, 뇌를 모방한 모델이라고 들 설명하지만 최성준 교수님은 다르게 생각을 하신다고 한다
(나 또한 공감)
무언가를 본따서 만들었다기 보단 이 자체로 생각을 하여
"Nonlinear Transformations(activation function)을 통하여 Function approximators(함수를 근사하는 모델)" 이라
해석하는 것이 더 좋은 표현인 것 같다
<Linear Neural Networks>
linear regression을 통한 NN으로 가장 간단한 모델이다


즉 X -> Y 를 선형모델로 한정 짓고 추론해내는 과정이다
어떻게 추론을 할 수 있을까??? -> BackPropagation 전략을 사용
(Gradient Descent)
loss function을 줄이는 것을 목표로 편미분(W와 b 에 대해)을 통해 업데이트 해나가는 방식으로 추론해낸다

<행렬에 관한 DL적 시선>
2개의 Vector Space간의 변환
즉, N차원의 벡터를 M차원으로 바꾸고 싶을 때 (두 차원의 선형변환) 행렬을 사용하면 된다
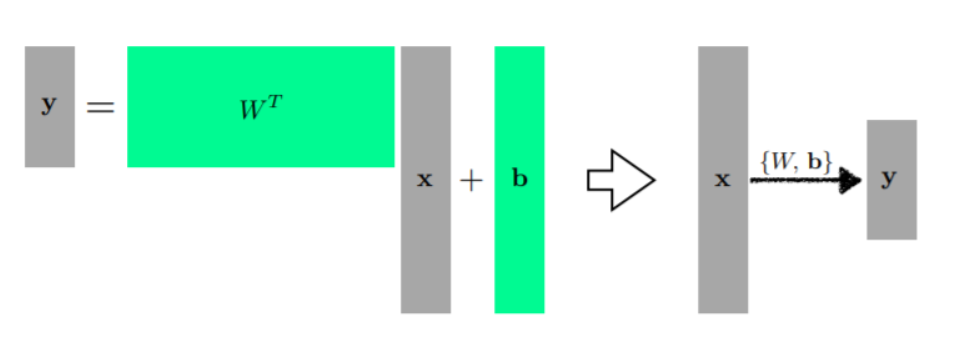
<왜 Deep? 일까???>
층을 쌓을 수 있어서 Deep이라는 표현을 사용하는 것 같다

이런 식으로 변환 을 하고 변환을 또 거칠 수가 있는데
여기에서 선형대수를 생각을 해본다면
Nonlinear transform을 거치지 않으면 W를 몇개를 쌓아도 한개랑 차이가 없다 $$ W_{3} = W_{1}W_{2} $$
즉, 네트워크의 표현력을 극대화 하기 위해서 다음과 같이 Nonlinear transform을 사용한다
$$Y = W_{1}\varphi (W_{2}X)$$
$$Y = W_{1}\varphi(W_{2}\varphi (W_{3}X)$$
다음과 같은 Nonlinear transform을 Activation Function 이라 한다
<Activation Function>
1. ReLU (가장 많이 사용)

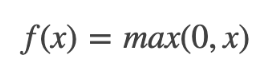
- x>0 이면 기울기가 1인 직선이고, x<0이면 함수값이 0이된다.
- sigmoid, tanh 함수와 비교시 학습이 훨씬 빠르다
- 연산 비용이 크지않고, 구현이 매우 간단하다.
- x<0인 값들에 대해서는 기울기가 0이기 때문에 뉴런이 죽을 수 있는 단점이 존재
2. Sigmoid



- 함수값이 (0, 1)로 제한된다.
- 중간 값은 1/2이다.
- 매우 큰 값을 가지면 함수값은 거의 1이며, 매우 작은 값을 가지면 거의 0이다.
- Gradient Vanishing 현상이 발생. 미분함수에 대해 x=0에서 최대값 1/4 을 가지고, X값이 일정이상 올라가면 미분값이 거의 0에 수렴하게 된다.
- 함수값 중심이 0이 아니다. 함수값 중심이 0이 아니라 학습이 느려질 수 있다.
3. tanh(Hyperbolic tangent function)

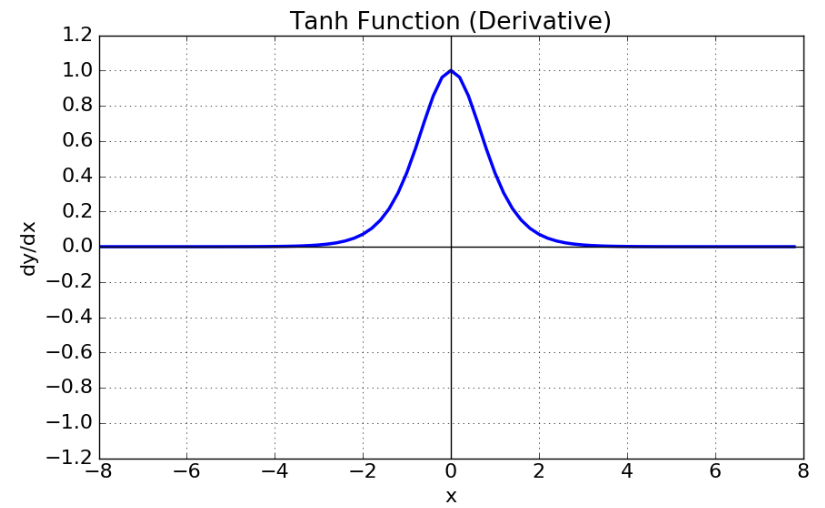
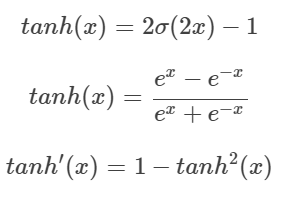
- 함수의 중심값을 0으로 옮겨 sigmoid의 최적화 과정이 느려지는 문제를 해결했다.
- gradient vanishing 문제는 여전히 남아있다.
<Loss Function>
입력이 주어질 때 해당 출력값과 데이터셋의 Target Data의 차이를 줄이는 것
1. Regression (MSE)
$$ MSE = \frac{1}{N}\sum_{i=1}^{N}\sum_{d=1}^{D}(y_{i}^{(d)}-\hat{y}_{i}^{(d)})^2 $$
-> 제곱이 있어서 이상치를 맞추다 네트워크가 망가질 수 있다 (그래서 MAE를 사용하기도 한다)
2. Classification (Cross-Entropy)
$$ CE = -\frac{1}{N}\sum_{i=1}^{N}\sum_{d=1}^{D}y_{i}^{(d)}log \hat{y}_{i}^{(d)} $$
내가 예측한 class의 출력값을 높이려 사용
(얼마나 높일 지는 중요 x, 어쩌피 d개 output중 가장 큰 놈 고르기 이기 때문) -> 다른 것과 차이만 두면 된다
분류 문제는 output으로 one-hot-vector를 사용하기 때문에 ex) {0,0,0,1,0,0,0,0,0}
예를 들어, 이미지를 읽어들여 개/고양이/물고기를 분류하는 3개의 클래스를 갖는 다중 분류 문제를 생각해보자. 가방에 개/고양이/물고기라고 쓰인 공이 들어있다. 이 공은 해당 이미지에 대한 정답을 사람이 적어 놓은 것이다. 예측 모형은 주어진 정보 (이미지) 를 살펴본 후, 예측 분포를 산출했는데, p(y) = [0.2, 0.3, 0.5] 으로 예측했다. 즉, 공 (실제 정답) 을 꺼냈을 때, 개/고양이/물고기를 관찰할 확률이 각각 0.2/0.3/0.5 일 것이라고 예측 한 것이다. 하지만 실제 분포, q(y) = [0, 0, 1] 이다. 이 때, cross-entropy 는 매우 간단하게, -log(0.5) 이다.
출처: https://3months.tistory.com/436 [Deep Play:티스토리]
3. Probabilistic (MLE)
확률적인 모델을 사용할 때 (출력값이 평균,분산 이런거 일 때)
$$MLE = \frac{1}{N}\sum_{i=1}^{N}\sum_{d=1}^{D}logN(y_{i}^{(d)} ; \hat{y}_{i}^{(d)}, 1)$$
가우시안의 log likelihood를 maximize하겠다