지수가중이동평균 (EWMA) Python 설명

EWMA (Exponentially Weighted Moving Average) : 지수가중이동평균

https://medium.com/aimonks/understanding-exponentially-weighted-moving-averages-ewma-cc8e78b01184

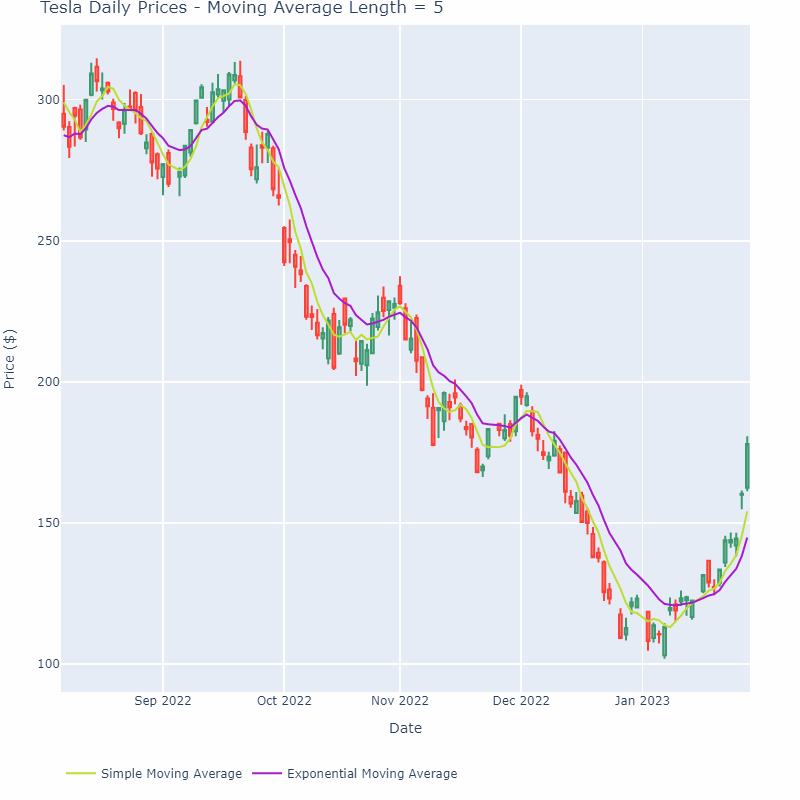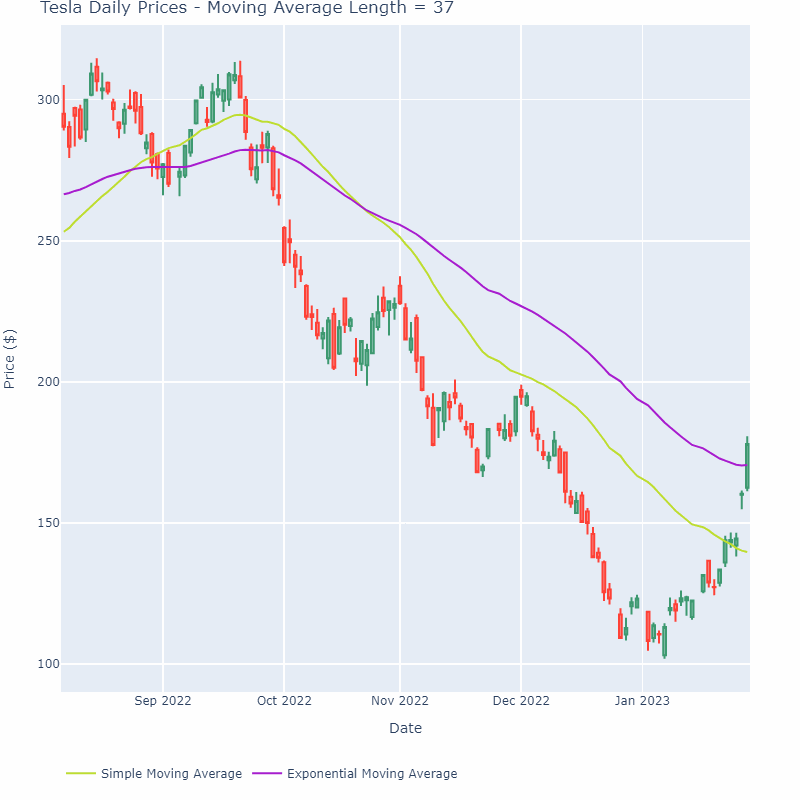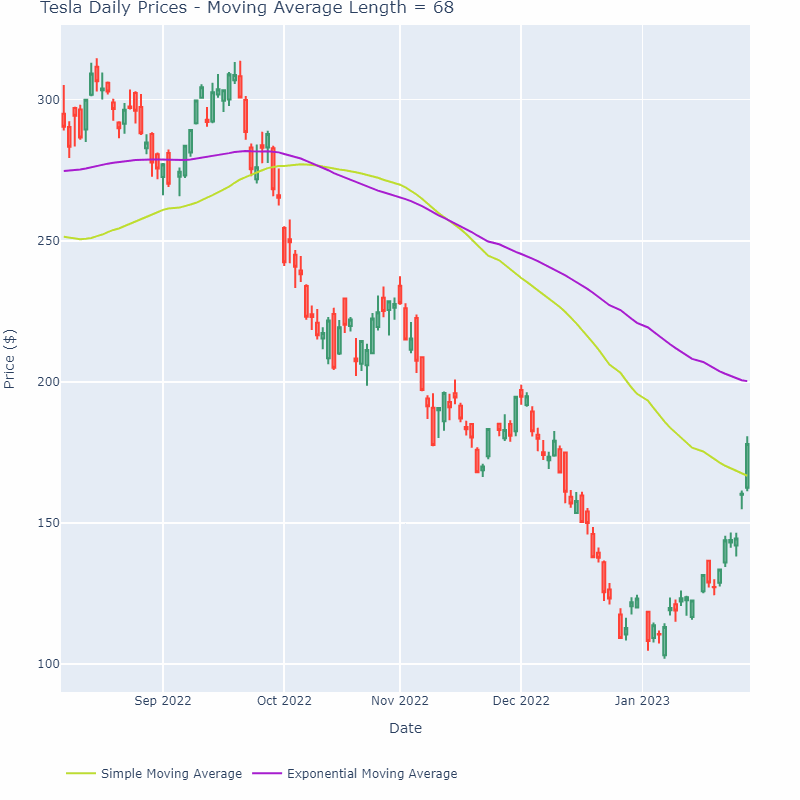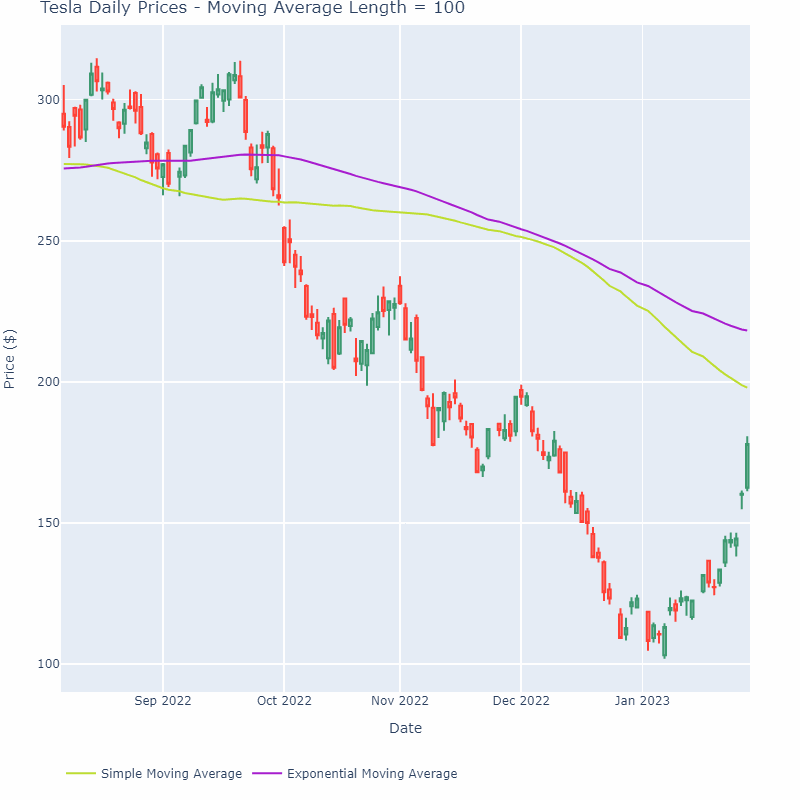
EWMA는 주로 시계열 데이터에 사용된다 (시간에 영향이 있는)

- 최근 데이터에서는 큰 비중(Weighted)을 적용하고 시간이 오래된 데이터에는 가중치를 적게 주는 방식

    - 여기에서 비중(Weighted)의 차이를 지수를 이용하여 (Exponentially) 구하게 된다

    - 만약 여기에서 비중 없이 일정한 가중치를 두게 된다면 그걸 (SMA : Simple Moving Average)라고 한다

다음 식을 보면 

t를 해당 시점이라고 생각 하고 a 가 0~ 1사이의 값을 가져서 곱해질 수록 작아진다는 관점으로 보면

새로운 데이터(최근 데이터) 가 나올 수록 과거의 데이터는 a가 계속 곱해지게 되며 작아지게 된다

 

즉, a가 커질 수록 점점 완만한 그래프가 그려지게 되는 것이다

 

또한 중요한 특징으로는 parameter를 a 만 가지는 것이다

 

EWMA hyperparameter

EWMA는 EWM + Average (Mean)를 이용해서 구할 수 있다

EWM은 다음과 같이 정의되어 있는데

    @final
    def ewm(
        self,
        com: float | None = None,
        span: float | None = None,
        halflife: float | None = None,
        alpha: float | None = None,
        min_periods: int = 0,
        adjust: _bool = True,
        ignore_na: _bool = False,
        axis: Axis = 0,
        times: np.ndarray | Series | None = None,
        method: CalculationMethod = "single",
    ) -> ExponentialMovingWindow[Series]: ...

 

이상한 점이 있다.

분명 patameter는 a만 가진다고 하였는데 나머지의 의미가 뭘까

 

결론부터 말하면 com, span, halflife는 a를 어떻게 구한지를 결정해주는 parameter이다

해당 링크(https://wikidocs.net/152787) 에 잘 설명되어 있지만 여기에 정리해 보자

 

 

a (alpha) 인수

간단히 말해서 아래 수식

에 있는 a에 다이렉트로 숫자를 꼽아 넣는 다는 것이다

그래서 0 ~ 1 사이의 값이여야 한다는 조건이 붙게 된다

t가 time인 것을 생각할 때 t, k 가 큰 것이 최신의 데이터라고 생각하면 이해가 빠르다

 

위에 수식을 전개하면 다음과 같이 된다

 

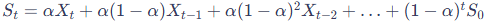
a  = 0.1 라고 할때

https://bruders.tistory.com/92

마지막 수식을 보면 0.1로 전체 수식을 묶었을 때 나머지는 1, 0.9, (0.9)^2, (0,9)^3 .... 이런식으로 전개가 된다.

극단적으로 a = 0.00...1 일때는 모두가 1,1,1,1 의 가중치를 가지게 된다

즉 a값이 작다면 과거의 영향이 커진다

 

a 가 1이였다면 과거 항에 있는 (1-a)의 영향으로 전부 없어지고 최신 데이터만 남게 된다

즉, a값이 크다면 최신의 영향이 커진다

 

이를 정리하면 다음과 같다

 

a가 크다 : 최신 영향, 그래프 요동, 변화에 민감 
a가 작다 : 과거 영향, 그래프 완만, 변화에 둔감

 

com 인수

com(Center of mass)은 "질량중심 감쇠법으로 평활계수를 계산하는 인수" 이다

수식은 : α = 1 / (1 + com) 이다

벌써 말이 어려운데

- 평활계수(a, alpha) : 새로운 데이터에 얼마만큼 반응할 것인가

- 질량중심 : 가중치의 중심을 얼마나 과거로 이동했는가 이다

 

즉, com = 0 이면 a =1  이 되므로 최신 데이터만 반영을 한다는 것이고

com = 1000 이면  a =0.00099 이 되면서 과거의 영향이 커진다

 

Center of mass 라는 단어로 본다면 과거에 비중을 얼마나 둘 것이냐라고 의역 할 수 있다

 

com : 과거의 비중을 얼마나 둘 것이냐
com이 크다 : a가 작다, 과거 영향
com이 작다 : a가 크다, 최신 영향

 

초록색이 빨강색 보다 com이 크다

 

span 인수

Span 의 경우 com과 수신이 매우 유사 하다

수식은 : α = 2 / (1 + Span) 이다

그래서 관계식은 Span = 2 x com + 1

여기서 의구심이 드는 것은 그럼 그냥 com을 쓰면 되지 왜 굳이 span을 쓸까?

단순히 표현의 차이이다

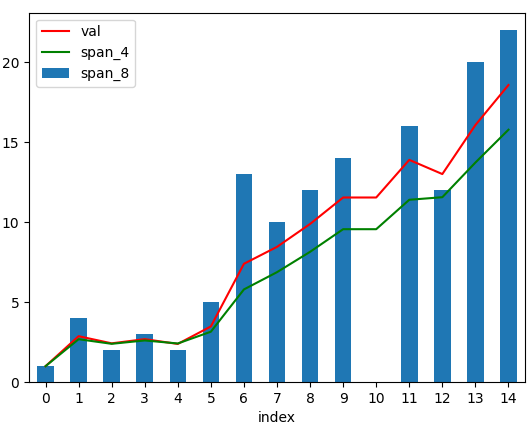
Span은 "대략 몇 개의 데이터의 영향을 반영할지"를 결정한다

 

Span : 몇 개의 데이터 영향을 받을 것인가
Span이 크다 : a가 작다, 과거 영향
Span이 작다 : a가 크다, 최신 영향

 

 

halflife 인수

halflife 의 수식을 보면 꽤나 복잡해 보인다

수식은 : α = 1 - e^(-ln(2)/halflife) 이다

그래도 자주 사용하는 이유는 의미가 있는 수치이기 때문이다

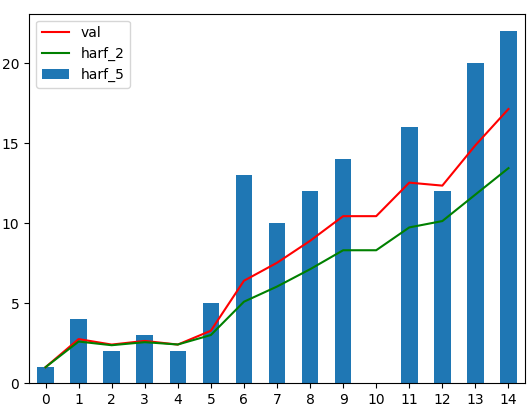
halflife는 "가중치가 절반으로 줄어드는데 걸리는 시간(샘플 수)를 의미 한다"

 

halflife : 가중치가 절반으로 줄어드는데 걸리는 샘플 수
halflife가 크다 : a가 작다, 과거 영향
halflife가 작다 : a가 크다, 최신 영향