[Generative] Diffusion에 관하여

관련 논문 :  Denoising Diffusion Probabilistic Models

https://arxiv.org/pdf/2006.11239.pdf

 

 

 

Diffusion 모델이란 데이터를 만들어내는 Deep generative model 중 하나이다

 

두가지 Process를 활용하는데

 

• Forward Process (Diffusion Process) : data로부터 noise를 조금씩 더해가면서 data를 완전한 noise로 만드는 process
• Reverse Process : noise를 조금씩 복원해가면서 data를 만들어내는 것

q : forward process /  p : reverse process (XT에서 X0로 복원하는 과정을 학습)

 

 

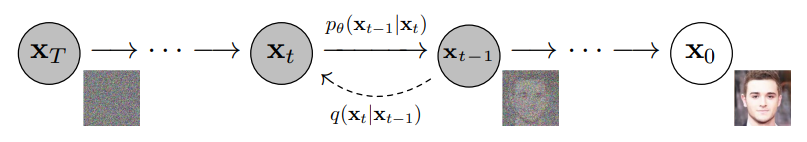
내용 이해를 위해서는 아래의 개념을 알아야 한다

 

Markov Chain

Markov Chain 은 간단하게 말해서 어떤 상태에서 다른 상태로 넘어갈 때, 바로 전 단계의 상태에만 영향을 받는 확률이다

한계점이 많지만 계산이 편해서 자주 사용하는데 다음과 같은 예시를 들어볼 수 있다

"내일 수능 시험은 오늘 공부를 얼마냐 하느냐에 따라 달려 있다" 

https://comdolidol-i.tistory.com/146

문제점은 : 초기의 분포의 영향이 시간이 지남에 따라 점점 감소한다는 것과 Stationary distribution (고정분포)를 가진다는 것이다

오랜 시간이 흐르면 Xt 분포가 더 이상 바뀌지 않는다는 것이다 

 

대충 이정도만 알고 넘어가자

 

 

Gaussian Noise

우리가 흔히 알고 있는 정규분포의 다른 말이 가우시안 분포이다

Gaussian Noise 적용 전과 후

이런 식으로 Gaussian Noise를 추가한다

 

 

Forward Process

Forward Process는 Data(x0)부터 noise를 더해 가면서 최종 noise(xT)를 만드는 것이다

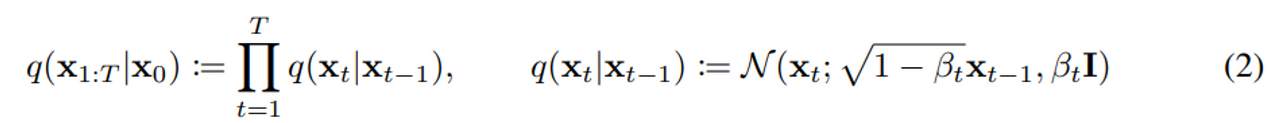
q 를 보면 바로 전 단계의 xt-1을 이용하여 정규분포를 사용하여서 만들어 내는 것을 볼 수 있다

위에 식에서 beta_t는 beta_1=10^{-4}에서 \beta_T=0.02까지 linear하게 증가하게 사전에 설정된다.

이 값을 변수가 아닌 상수로 지정한 이유는 별로 그렇게 차이가 없다는 것을 발견해서 그렇다고 한다

0.0001 에서 0.02 이므로 곱했을 때 둘다 값이 작아진다(signal 손상)

만약 T = 1000 이 되었을 때는 xT가 거의 Gaussian Distribution을 따르게 된다고 한다

\sqrt{1-\beta_t}로 scaling하는 이유는 variance를 unit으로 유지하기 위해서 이고

위에 같이 \sqrt{1-\beta_t}를 곱하고 나면 variance는 {1-\beta_t}가 되는데 이것이 beta_t와 더해지면서 unit variance가 된다

 

특징적인 것은 t에서의 xt 샘플링 할 수 있다는 것이다 (xt를 얻기 위해서 x0에서 부터 xt까지 구할 필요가 없다)

즉 t번에 sampling을 하지 않고 

어쩌피 계속 \sqrt{1-\beta_t} 와 {beta_t}가 곱해지는 꼴이니

위와 같이 나타낼 수 있다는 것이다

이러면 expectation을 구할 때 xt를 만들고 이에 대한 loss를 구한 다음 t에 대해 expectation을 구하는 식으로 학습할 수 있다

 

 

 

 

Reverse Process

Reverse Process p는 noise (XT)로 부터 Data(X0)를 복원하는 가정이다

이렇게 복원을 하는 과정은 random한 Noise로 부터 Data를 만들어 내는 Generative model이라 생각할 수 있으며이를 위해서 모델링해야 하지만 이를 실제로 할 수는 없기 때문에 Approximation(근사화)을 진행한다

이때 사용하는 Approximation은 Gaussian Transition을 활용한 Markov Chain 형태를 가지는데

Noise의 분포는 다음과 같이 표준정규분포를 따르고 시작 지점인 p(xT)는 다음과 같다

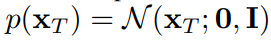
위에 있는 식과 같이 Pθ는 바로 전  단계인 xt를 조건부로 하는 xt-1의 확률로 정의가 되고

이를 위해서 우리는 θ에서의 

평균 μθ 와 표준편차 Σθ 를 Parameter로 학습을 해나간다

다음과 같이 mean과 variance를 파라미터로 가지는 이유는 이 둘이 Gaussian distribution의 parameter이고Forward Process에서 각 Step 마다 아주 작은 노이즈를 추가하는 것이라면 충분히 Gaussian Distribution을 통해 표현될 수 있다고 가정하기 때문이다

 

 

 

 

Training

우리가 하고자 하는 것은 pθ의 parameter를 추정하는 것인데 이를 어떻게 학습시키는지에 대해 나와 있다

우리는 따지고 보면 noise으로 부터 실제 data 분포인 p(x0)를 찾아내는 것을 목적으로 하고 이것과의 Likelihood를 최대화하는 방식으로 학습을 진행하면 된다.

 

 

 

이에 따라 Diffusion model의 최종적인 training loss는 다음과 같은데

 

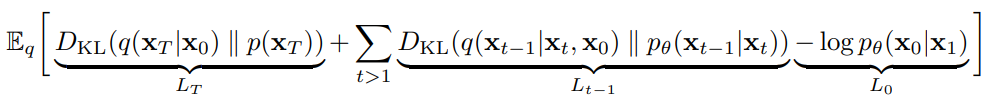
• LT: p가 generate하는 noise xT와 q가 x0라는 데이터가 주어졌을 때 generate하는 noise xT간의 분포 차이
• Lt−1: p와 q의 reverse / forward process의 분포 차이. 이들을 최대한 비슷한 방향으로 학습한다.  
• L0: latent x1으로부터 data x0를 추정하는 likelihood. 이를 maximize하는 방향으로 학습한다

 

중간에 증명도 나오고 유도하는 방법도 나오지만 결국 중요한 것은

Diffusion model을 학습할 때의 training loss는 정규 분포 사이의 KL divergence 형태로 계산이 가능하다는 것이다

 

<참고 자료>

https://sang-yun-lee.notion.site/Denoising-Diffusion-Probabilistic-Models-ade353a9abaa41d98c3ae2c18b52c129

Denoising Diffusion Probabilistic Models

 

 

https://process-mining.tistory.com/182

Diffusion model 설명 (Diffusion model이란? Diffusion model 증명)

https://lilianweng.github.io/posts/2021-07-11-diffusion-models/

What are Diffusion Models?

https://angeloyeo.github.io/2020/09/17/MCMC.html

Markov Chain Monte Carlo - 공돌이의 수학정리노트

 

 

 

<추가학습 자료> 

https://arxiv.org/pdf/2105.05233v4.pdf

 

Dall-e 2 : https://arxiv.org/pdf/2102.12092.pdf  (OpenAI)

Imagen : https://gweb-research-imagen.appspot.com/paper.pdf (Google Research, Brain)