SSIM의 정의
SSIM 은 Structural Similarity Index Measure의 약자로
다음 세가지를 이용하여서 두 이미지의 유사도를 계산한다
- luminance
- contrast
- structure
-> 실제 인간의 시각 기관과 유사한 방법으로 인식하고자 함
SSIM의 최종 결과는 0~1 사이이고 1에 가까울 수록 두 이미지가 유사하다는 의미이다 (가끔 -1 ~ 1 도 가능)
Luminance (휘도)
빛의 밝기를 의미
-> 빛의 밝기를 추출해서 사용하는 것이 아닌 grayscale로 변환한 다음 그 픽셀값을 이용 (값이 클수록 밝음)
만약 RGB에서 사용할 경우 R,G,B 각각의 채널 별 픽셀값을 이용한다
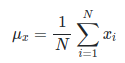
- : 각 픽셀의 값 (밝기 값을 의미함)
- : 전체 픽셀의 갯수
- : 이미지의 평균 밝기 (luminance)
이렇게 구한 이미지의 평균 밝기를 통해 두 이미지(x,y)사이의 luminance를 비교한다

여기서 C1은 분모가 0이 되는 것을 막기 위해 사용되는 상수라고 생각 (두 이미지가 같으면 값이 1 이 나오고 아예 다르면 0)

위 식에서 K1 는 일반 상수이며 보통 0.01을 사용.
L은 픽셀값의 범위를 입력하며 일반적으로 8비트 값을 사용하여 0 ~ 255의 픽셀 값을 사용하므로 255를 L로 사용.
주로 C1=(0.01×255)^2=6.5025을 사용.
Contrast (대조)
빛의 밝기가 바뀌는 정도
-> 픽셀 간의 값의 차이나 얼마나 나는 지를 정량화 해야하기 때문에 표준 편차를 이용
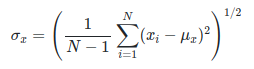
- : 각 픽셀의 값 (밝기 값을 의미함)
- : 전체 픽셀의 갯수
- : 이미지의 평균 밝기 (luminance)
N-1 을 사용하는 이유는 포본의 표준 편차를 구하기 위해서 1을 빼준다
이렇게 구한 표준편차를 luminance와 동일하게 비교한다

여기서 C2은 분모가 0이 되는 것을 막기 위해 사용되는 상수라고 생각 (두 이미지가 같으면 값이 1 이 나오고 아예 다르면 0)

위 식에서 K2 는 일반 상수이며 보통 0.03을 사용.
L은 픽셀값의 범위를 입력하며 일반적으로 8비트 값을 사용하여 0 ~ 255의 픽셀 값을 사용하므로 255를 L로 사용.
주로 C2=(0.03×255)^2=58.5225을 사용.
Structure (구조적 차이점)
픽셀값의 구조적인 차이점을 나타내며 성분을 확인시 edge를 나타냄
-> structure를 계산 하기위해 luminance를 평균 , contrast를 표준편차로 Normalized된 픽셀 값의 분포에서 픽셀 값 을 재정의

두 이미지의 Structure의 유사성을 이용한다는 것 = 두 이미지의 Correlation 을 이용한다(상관관계)
Correlation : 두 개 변수가 일정 비율로 함께 변하는 정도

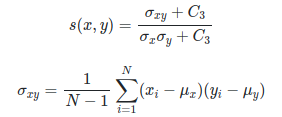
C3는 편의상 C2/2로 사용 (이유는 밑에 SSIM을 구하는 과정에서 나옴)
SSIM
위에서 구한 Luminance, Contrast, Structure를 모두 반영하여서 이미지의 유사도를 결정하는 방법이 SSIM이다

만약 a,B,r 모두 1이라고 가정을 하고 C3=C2/2 이라고 하면

만약 RGB에서 SSIM을 이용하고자 한다면 다음과 같이 각 채널별로 SSIM을 구한 후에 모두 합쳐주면 된다

일반적으로 w를 모두 1/3 으로 균등한 가중치를 주지만 특정 채널에 대해 가중치를 더 줄 수도 있다
(ex: YCrCb : Y=0.8, Cr = 0.1, Cb = 0.1)
https://dsp.stackexchange.com/questions/75187/how-to-apply-the-ssim-measure-on-rgb-images
SSIM 사용법
SSIM을 이미지 전체를 한번에 확인하는 방법은 효과가 떨어진다
그래서 NxN window를 이용하여서 locally하게 비교를 하는 것이 더 효율 적이다
(통계적특성이 더 잘 나타나고 다양한 특성을 분석할 수 있기 때문에)
또한 SSIM을 Loss로 활용할 수 도 있는데 (미분이 가능하기때문)

으로 한다면 이미지 유사도가 낮을 수록 높은 loss를 줄 수 있다
코드
(다음 출처 에서 가져왔다)
Pytorch (전체 이미지)
class SSIM(nn.Module):
"""Layer to compute the SSIM loss between a pair of images
"""
def __init__(self):
super(SSIM, self).__init__()
self.mu_x_pool = nn.AvgPool2d(3, 1)
self.mu_y_pool = nn.AvgPool2d(3, 1)
self.sig_x_pool = nn.AvgPool2d(3, 1)
self.sig_y_pool = nn.AvgPool2d(3, 1)
self.sig_xy_pool = nn.AvgPool2d(3, 1)
# 입력 경계의 반사를 사용하여 상/하/좌/우에 입력 텐서를 추가로 채웁니다.
self.refl = nn.ReflectionPad2d(1)
self.C1 = 0.01 ** 2
self.C2 = 0.03 ** 2
def forward(self, x, y):
# shape : (xh, xw) -> (xh + 2, xw + 2)
x = self.refl(x)
# shape : (yh, yw) -> (yh + 2, yw + 2)
y = self.refl(y)
mu_x = self.mu_x_pool(x)
mu_y = self.mu_y_pool(y)
sigma_x = self.sig_x_pool(x ** 2) - mu_x ** 2
sigma_y = self.sig_y_pool(y ** 2) - mu_y ** 2
sigma_xy = self.sig_xy_pool(x * y) - mu_x * mu_y
SSIM_n = (2 * mu_x * mu_y + self.C1) * (2 * sigma_xy + self.C2)
SSIM_d = (mu_x ** 2 + mu_y ** 2 + self.C1) * (sigma_x + sigma_y + self.C2)
# SSIM score
return torch.clamp((SSIM_n / SSIM_d) / 2, 0, 1)
# Loss function
# return torch.clamp((1 - SSIM_n / SSIM_d) / 2, 0, 1)Pytorch (window 방식)
convolution 방식을 사용함
import torch
import torch.nn.functional as F
import numpy as np
import math
import cv2
def gaussian(window_size, sigma):
#가우시안 분포를 출력
"""
Generates a list of Tensor values drawn from a gaussian distribution with standard
diviation = sigma and sum of all elements = 1.
Length of list = window_size
"""
gauss = torch.Tensor([math.exp(-(x - window_size//2)**2/float(2*sigma**2)) for x in range(window_size)])
return gauss/gauss.sum()
def create_window(window_size, channel=1):
#local영역을 순회하는 window를 만듬
# Generate an 1D tensor containing values sampled from a gaussian distribution
# _1d_window : (window_size, 1)
# sum of _1d_window = 1
_1d_window = gaussian(window_size=window_size, sigma=1.5).unsqueeze(1)
# Converting to 2D : _1d_window (window_size, 1) @ _1d_window.T (1, window_size)
# _2d_window : (window_size, window_size)
# sum of _2d_window = 1
_2d_window = _1d_window.mm(_1d_window.t()).float().unsqueeze(0).unsqueeze(0)
# expand _2d_window to window size
# window : (channel, 1, window_size, window_size)
window = torch.Tensor(_2d_window.expand(channel, 1, window_size, window_size).contiguous())
return window
def ssim(img1, img2, window_size=11, val_range=255, window=None, size_average=True, full=False):
# L is the dynamic range of the pixel values (255 for 8-bit grayscale images),
L = val_range
try:
_, channels, height, width = img1.size()
except:
channels, height, width = img1.size()
# if window is not provided, init one
if window is None:
# window should be at least 11x11
real_size = min(window_size, height, width)
window = create_window(real_size, channel=channels).to(img1.device)
# calculating the mu parameter (locally) for both images using a gaussian filter
# calculates the luminosity params
pad = window_size//2
mu1 = F.conv2d(img1, window, padding=pad, groups=channels)
#local 영역의 평균과 표준편차를 구함
mu2 = F.conv2d(img2, window, padding=pad, groups=channels)
mu1_sq = mu1 ** 2
mu2_sq = mu2 ** 2
mu12 = mu1 * mu2
# now we calculate the sigma square parameter
# Sigma deals with the contrast component
sigma1_sq = F.conv2d(img1 * img1, window, padding=pad, groups=channels) - mu1_sq
sigma2_sq = F.conv2d(img2 * img2, window, padding=pad, groups=channels) - mu2_sq
sigma12 = F.conv2d(img1 * img2, window, padding=pad, groups=channels) - mu12
# Some constants for stability
C1 = (0.01 ) ** 2 # NOTE: Removed L from here (ref PT implementation)
C2 = (0.03 ) ** 2
contrast_metric = (2.0 * sigma12 + C2) / (sigma1_sq + sigma2_sq + C2)
contrast_metric = torch.mean(contrast_metric)
numerator1 = 2 * mu12 + C1
numerator2 = 2 * sigma12 + C2
denominator1 = mu1_sq + mu2_sq + C1
denominator2 = sigma1_sq + sigma2_sq + C2
ssim_score = (numerator1 * numerator2) / (denominator1 * denominator2)
if size_average:
ret = ssim_score.mean()
else:
ret = ssim_score.mean(1).mean(1).mean(1)
if full:
return ret, contrast_metric
return ret
Scikitlearn 활용
https://scikit-image.org/docs/stable/api/skimage.metrics.html#skimage.metrics.structural_similarity
skimage.metrics — skimage 0.21.0 documentation
[1] (1,2,3) Wang, Z., Bovik, A. C., Sheikh, H. R., & Simoncelli, E. P. (2004). Image quality assessment: From error visibility to structural similarity. IEEE Transactions on Image Processing, 13, 600-612. https://ece.uwaterloo.ca/~z70wang/publications/ssim
scikit-image.org
origin 이미지와 노이즈가 추가된 이미지 3개(noise 1,2,3 )를 비교
import cv2
import matplotlib.pyplot as plt
from skimage.metrics import structural_similarity as ssim
origin = cv2.cvtColor(cv2.imread("origin.png"), cv2.COLOR_BGR2RGB)
noise1 = cv2.cvtColor(cv2.imread("noise1.png"), cv2.COLOR_BGR2RGB)
noise2 = cv2.cvtColor(cv2.imread("noise2.png"), cv2.COLOR_BGR2RGB)
noise3 = cv2.cvtColor(cv2.imread("noise3.png"), cv2.COLOR_BGR2RGB)
ssim_1, diff1 = ssim(origin, noise1, channel_axis=2, full=True)
diff1 = (diff1 * 255).astype("uint8")
# plt.imshow(diff1)
ssim_2, diff2 = ssim(origin, noise2, channel_axis=2, full=True)
diff2 = (diff2 * 255).astype("uint8")
ssim_3, diff3 = ssim(origin, noise3, channel_axis=2, full=True)
diff3 = (diff3 * 255).astype("uint8")
print(ssim_1, ssim_2, ssim_3)
# 0.21075336301148573 0.6888119020545118 0.7808179172891382
ssim_1, diff1 = ssim(origin, noise1, channel_axis=2, win_size=11, full=True)
diff1 = (diff1 * 255).astype("uint8")
ssim_2, diff2 = ssim(origin, noise2, channel_axis=2, win_size=11, full=True)
diff2 = (diff2 * 255).astype("uint8")
ssim_3, diff3 = ssim(origin, noise3, channel_axis=2, win_size=11, full=True)
diff3 = (diff3 * 255).astype("uint8")
print(ssim_1, ssim_2, ssim_3)
# 0.23226598957553168 0.7078116166774144 0.7831195478428952
결과 영상
AI보다 속도도 빠르고 정확했다
segmentation으로 별간 고생했지만
솔루션은 SSIM 이였던 것
https://youtu.be/Dc0SUQcaEZU?si=4-nvJ2auNTThWvtE
참고자료
https://gaussian37.github.io/vision-concept-ssim/
SSIM (Structural Similarity Index)
gaussian37's blog
gaussian37.github.io
'프로젝트 모음 > HRI ROS Project' 카테고리의 다른 글
| [Robotics][Proj 18] Segmentation 모델(mmsegmentation) 준비 및 적용 (0) | 2023.06.27 |
|---|---|
| [Robotics][Proj 17] semantic segmentation 예제 연습 (1) | 2023.06.09 |
| [Robotics][Proj 16] Print 문 커스텀 (0) | 2023.05.25 |
| [Robotics][Proj 15] Raspberry pi CLI 환경 고정IP (0) | 2023.05.23 |
| [Robotics][Proj 14] Roslaunch로 Rosrun 묶기 (0) | 2023.05.19 |



