[AI Math]모수 와 (표집분포, 표본분포, 모집단)의 기대값과 분산

통계적 모델링

적절한 가정 위에서 확률분포를 추정(inference)하는 것

-> 데이터를 모으는 데 한계가 있으므로 근사적으로 확률분포를 추정할 수 밖에 없다

 

모수적 방법론 (parametric)

1. 특정 확률분포(ex 정규, 베르누이,카테고리...)를 따른 다고 가정한 다음

2. 그 확률분포의 모수(parameter)를 추정하는 방법

 

* 모수??

확률분포를 결정하는 애들이 모수(parameter) ex) 정규분포 -> 평균, 분산

나무 위키

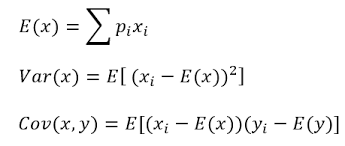
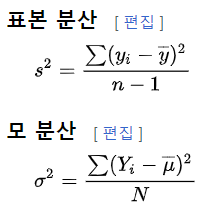
* 확률 분포의 종류 ( -> 히스토그램을 보고 결정하기)

베르누이 분포: 데이터가 두개 (0,1)

카테고리 분포: 데이터가 n개 (이산적)

베타 분포:        데이터가 [0,1]사이의 값

감마분포:         데이터가 0 이상의 값 (+로그정규분포)

정규분포:         데이터가 실수 전체의 값을 가지는 경우 (+라플라스분포)

 

정규 분포

확률 밀도 f(x)가 다음과 같을때 정규분포 N(μ, σ²/N)

 

 

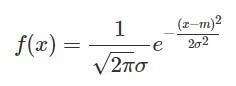
표본이란? :

모집단 중 대표할 수 있는 집단을 선별(부분집단)

표본평균                                      표본분산

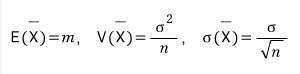
표본 분산의 N이 아니라 N-1로 나누는 이유 : 불편(unbiased) 추정량을 구하기 위함

 

 

 

표집 분포(Sampling Distribution)

(통계량의 확률분포) -> 표본들의 분포 x

ex) 정규분포의 표집분포 : 표본평균과 표분분산의 확률분포

 

중심극한정리(Central Limit Theorem)

표집분포는 N이 커질 수록 정규분포 N(μ, σ²/N)을 따른다 

=> 모집단의 분포가 정규분포를 따르지 않아도 성립

(ex 베르누이(이항)분포 : N이 아무리 커져도 정규분포가 되지 않지만 표집분포는 정규분포처럼 된다)