

단순하게 생각을 하면 쉽다
<경사상승법 (Gradient Ascent)>
함수값을 증가하고 싶으면 미분 값을 더하면 된다
증가함수 일때 (x축 오른쪽에 있을 수록 큰 값): 미분값 (양수) + :더하면 x축의 오른쪽으로 이동 -> 증가
감소함수 일때 (x축 오른쪽에 있을 수록 작은 값): 미분값 (음수) + :더하면 x축의 왼쪽으로 이동 -> 증가
<경사하강법 (Gradient Descent)>
함수값을 감소하고 싶으면 미분 값을 빼면 된다
증가함수 일때 (x축 오른쪽에 있을 수록 큰 값): 미분값 (양수) + :더하면 x축의 왼쪽으로 이동 -> 감소
감소함수 일때 (x축 오른쪽에 있을 수록 작은 값): 미분값 (음수) + :더하면 x축의 오른쪽으로 이동 -> 감소
즉,
<Gradient Descent 방법을 딥러닝에 사용한다?>
어떤 모델에 input x 가 들어올 때 그거에 대한 loss가 구해질 때 이 loss를 낮아지게 끔 Weight를 업데이트 하는 방법
고려해야할 요소
1. Weight & Parameter
2. Starting Point
3. Step Size (learning rate)
4. Cost & Loss
Pytorch 이용 (torch.optim) -> 함수가 대부분 내장되어 있다
# example 1
optimizer = optim.SGD(model.parameters(), lr = 0.001, momentum = 0.9)
# example 2
optimizer = optim.Adam([var1,var2], lr = 0.0001)와 같이 내장 함수를 이용할 수 있다
(요즘은 주로 Adam을 사용한다)
Optimizer??
최적화(Optimization)은 손실 함수(Loss Function)의 결과값을 최소화하는 모델의 파라미터(가중치)를 찾는 것을 의미한다. 그리고 Optimization의 알고리즘을 Optimizer라고 한다.
실습
첫번째 : 딥러닝을 이용하여서 x을 업데이트 하며 수식을 만족하는 y를 찾아가 보자
1. Fθ(x)를 정의 (θ를 모수로 가지는 모델)
2. 미분 당할 loss function을 정의
3. Gradient Descent 정의
1. 함수를 정의해보자
def func(val):
fun = sym.poly(x**2 + 2*x + 3)
return fun.subs(x,val), fun #x에 val를 넣은 값, fun 수식을 return
#ex)
print(func(2))
#(11, Poly(x**2 + 2*x + 3, x, domain='ZZ'))2. 미분하는 loss function 정의
def func_gradient(fun, val):
_, function = fun(val)
diff = sym.diff(function, x)
return diff.subs(x, val), diff
#다음과 같이 미분의 정의를 이용하여서 구할 수도 있다
#컴퓨터로는 h -> 0 을 구현 할 수 없으므로 1e-9로 대신한다(우극한 사용)
def func_gradient(fun,x, h = 1e-9):
diff = (f(x+h) - f(x))/h
return diff.subs(x, val), diff함수의 도함수에 val를 넣은 식과, 도함수를 return 해준다
3. Gradient Descent 정의
def gradient_descent(fun, init_point, lr_rate=1e-2, epsilon=1e-5):
cnt = 0
val = init_point
diff, _ = func_gradient(fun, val)
# 함수의 최소점(optimal point) 근처로 충분히 가까이 올 때까지 loop
while np.abs(diff) > epsilon:
val = val - lr_rate*diff
diff, _ = func_gradient(fun, val)
cnt += 1
print("함수: {}\n연산횟수: {}\n최소점: ({}, {})".format(fun(val)[1], cnt, val, fun(val)[0]))epsilon의 조건을 초반에 선언을 해주어서 ending point 를 지정해 준다(while문을 빠질 수 있게 해줌)
np.random.choice(1000,10,replace = True)numpy.random.choice(a, size=None, replace=True, p=None)
- a : 1차원 배열 또는 정수 (정수인 경우, np.arange(a) 와 같은 배열 생성)
- size : 정수 또는 튜플(튜플인 경우, 행렬로 리턴됨. (m, n, k) -> m * n * k), optional
- replace : 중복 허용 여부, boolean, optional
- p : 1차원 배열, 각 데이터가 선택될 확률, optional
이를 이용해서
Linear Regression을 구현할 수 있다
-> loss = MSE 혹은 L2-norm을 사용
train_x = (np.random.rand(1000) - 0.5) * 10
train_y = np.zeros_like(train_x) #초기화
def func(val):
fun = sym.poly(7*x + 2)
return fun.subs(x, val)
# label 생성
for i in range(1000):
train_y[i] = func(train_x[i])
# initialize
w, b = 0.0, 0.0
lr_rate = 1e-2
n_data = len(train_x)
errors = []
for i in range(100):
_y = train_x * w + b
#MSE
error = np.sum((_y - train_y) ** 2) / n_data
#이건 MSE이고 L2-norm을 이용하려면 root를 씌워주면 된다
#_y = train_x * w + b
gradient_w = np.sum((_y - train_y) * train_x) / n_data #train_x는 속미분 때문에 나오고 앞에 2는 그냥 생략(lr 로 커버가 가능)
gradient_b = np.sum((_y - train_y)) / n_data #위의 식을 b에 대해 미분
# w와 b에 대하여 각각 gradient descent 적용
w -= lr_rate * gradient_w
b -= lr_rate * gradient_b
#lr를 다르게 할 수도 있긴 하지만 요즘은 그러지는 않음
# plot으로 확인하기 위함
errors.append(error)
print("w : {} / b : {} / error : {}".format(w, b, error))
다음과 같이 다항함수 일때 Linear Regression 진행
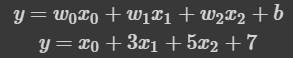
train_x = np.array([[1,1,1], [1,1,2], [1,2,2], [2,2,3], [2,3,3], [1,2,3]])
train_y = np.dot(train_x, np.array([1,3,5])) + 7
# random initialize
beta_gd = [9.4, 10.6, -3.7, -1.2]
# 상수항까지 한번에 matrix multiplication으로 계산하기 위해 expand (bias 때문에 1을 추가해줌, x를 weight로 보기)
expand_x = np.array([np.append(x, [1]) for x in train_x])
print("expand_X : \n", expand_x)
print("--------------")
for t in range(5000):
pred_y = expand_x @ beta_gd
error = train_y - pred_y
# matmul을 통해 gradient를 한번에 계산 (beta_gd의 gradient)
grad = -np.transpose(expand_x) @ error # numpy.matmul (@ operator)
#https://cyber0946.tistory.com/64
# lr_rate = 0.01
beta_gd = beta_gd - 0.01 * grad
print("After gradient descent, beta_gd : {}".format(beta_gd))expand_X : [[1 1 1 1] [1 1 2 1] [1 2 2 1] [2 2 3 1] [2 3 3 1] [1 2 3 1]]
SGD (Stochastic Gradient Descent) + mini-batch
train_x = (np.random.rand(1000) - 0.5) * 10
train_y = np.zeros_like(train_x)
def func(val):
fun = sym.poly(7*x + 2)
return fun.subs(x, val)
# label 생성
for i in range(1000):
train_y[i] = func(train_x[i])
# initialize
w, b = 0.0, 0.0
lr_rate = 1e-2
n_data = 10
errors = []
for i in range(100):
# mini batch 생성
idx = np.random.choice(1000, 10, replace=False) #idx의 중복을 허용하지 않기 위해서
mini_x = train_x[idx]
mini_y = train_y[idx]
_y = mini_x * w + b
error = np.sum((_y - mini_y) ** 2) / n_data
#코드 상으로 error가 밑에 영향을 주지 않기는 함
gradient_w = np.sum((_y - mini_y) * mini_x) / n_data
gradient_b = np.sum((_y - mini_y)) / n_data
w -= lr_rate * gradient_w
b -= lr_rate * gradient_b
# Error graph 출력하기 위한 부분
errors.append(error)
print("w : {} / b : {} / error : {}".format(w, b, error))- SGD는 GD에 비하여 수렴속도 가 빠르다
- mini-batch의 경우, 매 epoch마다 mini-batch를 sampling해서 GD를 하기 때문에 그래프가 매끄럽지 않지만, 그만큼 초기에 빠르게 minimum으로 수렴하는 것을 확인할 수 있습니다.
- GD : 전체 샘플들을 반복적으로 업데이트(수정)한다.
- SGD : 하나의 샘플만을 반복적으로 업데이트 한다.
'Math' 카테고리의 다른 글
| [AI Math][심화] Maximum Likelihood Estimation(MLE) (0) | 2022.10.04 |
|---|---|
| [AI Math]모수 와 (표집분포, 표본분포, 모집단)의 기대값과 분산 (0) | 2022.09.26 |
| [AI Math]Monte Carlo Sampling(몬테카를로 샘플링) (0) | 2022.09.22 |
| [AI Math]L1- norm, L2-norm 에 관하여 (0) | 2022.09.22 |
![[AI Math][심화] Gradient Descent](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FeL5AxC%2FbtrNyGARa82%2Fk2hkHFW4as37ylZiAukf10%2Fimg.png)